Utility Functions¶
These modules contain common utility and helper functions for B-Spline / NURBS curve and surface evaluation operations.
Utilities¶
The utilities module contains common utility functions for NURBS-Python library and its extensions.
-
geomdl.utilities.check_params(params)¶ Checks if the parameters are defined in the domain [0, 1].
Parameters: params (list, tuple) – parameters (u, v, w) Returns: True if defined in the domain [0, 1]. False, otherwise. Return type: bool
-
geomdl.utilities.color_generator(seed=None)¶ Generates random colors for control and evaluated curve/surface points plots.
The
seedargument is used to set the random seed by directly passing the value torandom.seed()function. Please see the Python documentation for more details on therandommodule .Inspired from https://stackoverflow.com/a/14019260
Parameters: seed – Sets the random seed Returns: list of color strings in hex format Return type: list
-
geomdl.utilities.evaluate_bounding_box(ctrlpts)¶ Computes the minimum bounding box of the point set.
The (minimum) bounding box is the smallest enclosure in which all the input points lie.
Parameters: ctrlpts (list, tuple) – points Returns: bounding box in the format [min, max] Return type: tuple
-
geomdl.utilities.make_quad(points, size_u, size_v)¶ Converts linear sequence of input points into a quad structure.
Parameters: - points (list, tuple) – list of points to be ordered
- size_v (int) – number of elements in a row
- size_u (int) – number of elements in a column
Returns: re-ordered points
Return type: list
-
geomdl.utilities.make_quadtree(points, size_u, size_v, **kwargs)¶ Generates a quadtree-like structure from surface control points.
This function generates a 2-dimensional list of control point coordinates. Considering the object-oriented representation of a quadtree data structure, first dimension of the generated list corresponds to a list of QuadTree classes. Second dimension of the generated list corresponds to a QuadTree data structure. The first element of the 2nd dimension is the mid-point of the bounding box and the remaining elements are corner points of the bounding box organized in counter-clockwise order.
To maintain stability for the data structure on the edges and corners, the function accepts
extrapolatekeyword argument. If it is True, then the function extrapolates the surface on the corners and edges to complete the quad-like structure for each control point. If it is False, no extrapolation will be applied. By default,extrapolateis set to True.Please note that this function’s intention is not generating a real quadtree structure but reorganizing the control points in a very similar fashion to make them available for various geometric operations.
Parameters: - points (list, tuple) – 1-dimensional array of surface control points
- size_u (int) – number of control points on the u-direction
- size_v (int) – number of control points on the v-direction
Returns: control points organized in a quadtree-like structure
Return type: tuple
-
geomdl.utilities.make_zigzag(points, num_cols)¶ Converts linear sequence of points into a zig-zag shape.
This function is designed to create input for the visualization software. It orders the points to draw a zig-zag shape which enables generating properly connected lines without any scanlines. Please see the below sketch on the functionality of the
num_colsparameter:num cols <-=============-> ------->>-------| |------<<-------| |------>>-------| -------<<-------|
Please note that this function does not detect the ordering of the input points to detect the input points have already been processed to generate a zig-zag shape.
Parameters: - points (list) – list of points to be ordered
- num_cols (int) – number of elements in a row which the zig-zag is generated
Returns: re-ordered points
Return type: list
Helpers¶
The helpers module contains common functions required for evaluating both surfaces and curves, such as basis
function computations, knot vector span finding, etc.
-
geomdl.helpers.basis_function(degree, knot_vector, span, knot)¶ Computes the non-vanishing basis functions for a single parameter.
Implementation of Algorithm A2.2 from The NURBS Book by Piegl & Tiller. Uses recurrence to compute the basis functions, also known as Cox - de Boor recursion formula.
Parameters: - degree (int) – degree,
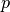
- knot_vector (list, tuple) – knot vector,
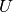
- span (int) – knot span,
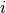
- knot (float) – knot or parameter,
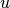
Returns: basis functions
Return type: list
- degree (int) – degree,
-
geomdl.helpers.basis_function_all(degree, knot_vector, span, knot)¶ Computes all non-zero basis functions of all degrees from 0 up to the input degree for a single parameter.
A slightly modified version of Algorithm A2.2 from The NURBS Book by Piegl & Tiller. Wrapper for
helpers.basis_function()to compute multiple basis functions. Uses recurrence to compute the basis functions, also known as Cox - de Boor recursion formula.For instance; if
degree = 2, then this function will compute the basis function values of degrees 0, 1 and 2 for theknotvalue at the input knotspanof theknot_vector.Parameters: - degree (int) – degree,
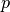
- knot_vector (list, tuple) – knot vector,
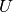
- span (int) – knot span,
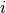
- knot (float) – knot or parameter,
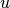
Returns: basis functions
Return type: list
- degree (int) – degree,
-
geomdl.helpers.basis_function_ders(degree, knot_vector, span, knot, order)¶ Computes derivatives of the basis functions for a single parameter.
Implementation of Algorithm A2.3 from The NURBS Book by Piegl & Tiller.
Parameters: - degree (int) – degree,
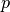
- knot_vector (list, tuple) – knot vector,
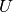
- span (int) – knot span,
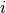
- knot (float) – knot or parameter,
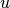
- order (int) – order of the derivative
Returns: derivatives of the basis functions
Return type: list
- degree (int) – degree,
-
geomdl.helpers.basis_function_ders_one(degree, knot_vector, span, knot, order)¶ Computes the derivative of one basis functions for a single parameter.
Implementation of Algorithm A2.5 from The NURBS Book by Piegl & Tiller.
Parameters: - degree (int) – degree,
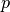
- knot_vector (list, tuple) – knot_vector,
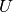
- span (int) – knot span,
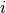
- knot (float) – knot or parameter,
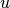
- order (int) – order of the derivative
Returns: basis function derivatives
Return type: list
- degree (int) – degree,
-
geomdl.helpers.basis_function_one(degree, knot_vector, span, knot)¶ Computes the value of a basis function for a single parameter.
Implementation of Algorithm 2.4 from The NURBS Book by Piegl & Tiller.
Parameters: - degree (int) – degree,
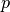
- knot_vector (list, tuple) – knot vector
- span (int) – knot span,
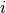
- knot (float) – knot or parameter,
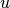
Returns: basis function,
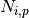
Return type: float
- degree (int) – degree,
-
geomdl.helpers.basis_functions(degree, knot_vector, spans, knots)¶ Computes the non-vanishing basis functions for a list of parameters.
Wrapper for
helpers.basis_function()to process multiple span and knot values. Uses recurrence to compute the basis functions, also known as Cox - de Boor recursion formula.Parameters: - degree (int) – degree,
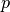
- knot_vector (list, tuple) – knot vector,
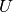
- spans (list, tuple) – list of knot spans
- knots (list, tuple) – list of knots or parameters
Returns: basis functions
Return type: list
- degree (int) – degree,
-
geomdl.helpers.basis_functions_ders(degree, knot_vector, spans, knots, order)¶ Computes derivatives of the basis functions for a list of parameters.
Wrapper for
helpers.basis_function_ders()to process multiple span and knot values.Parameters: - degree (int) – degree,
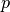
- knot_vector (list, tuple) – knot vector,
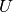
- spans (list, tuple) – list of knot spans
- knots (list, tuple) – list of knots or parameters
- order (int) – order of the derivative
Returns: derivatives of the basis functions
Return type: list
- degree (int) – degree,
-
geomdl.helpers.curve_deriv_cpts(dim, degree, kv, cpts, rs, deriv_order=0)¶ Compute control points of curve derivatives.
Implementation of Algorithm A3.3 from The NURBS Book by Piegl & Tiller.
Parameters: - dim (int) – spatial dimension of the curve
- degree (int) – degree of the curve
- kv (list, tuple) – knot vector
- cpts (list, tuple) – control points
- rs – minimum (r1) and maximum (r2) knot spans that the curve derivative will be computed
- deriv_order (int) – derivative order, i.e. the i-th derivative
Returns: control points of the derivative curve over the input knot span range
Return type: list
-
geomdl.helpers.degree_elevation(degree, ctrlpts, **kwargs)¶ Computes the control points of the rational/non-rational spline after degree elevation.
Implementation of Eq. 5.36 of The NURBS Book by Piegl & Tiller, 2nd Edition, p.205
- Keyword Arguments:
num: number of degree elevations
Please note that degree elevation algorithm can only operate on Bezier shapes, i.e. curves, surfaces, volumes.
Parameters: - degree (int) – degree
- ctrlpts (list, tuple) – control points
Returns: control points of the degree-elevated shape
Return type: list
-
geomdl.helpers.degree_reduction(degree, ctrlpts, **kwargs)¶ Computes the control points of the rational/non-rational spline after degree reduction.
Implementation of Eqs. 5.41 and 5.42 of The NURBS Book by Piegl & Tiller, 2nd Edition, p.220
Please note that degree reduction algorithm can only operate on Bezier shapes, i.e. curves, surfaces, volumes and this implementation does NOT compute the maximum error tolerance as described via Eqs. 5.45 and 5.46 of The NURBS Book by Piegl & Tiller, 2nd Edition, p.221 to determine whether the shape is degree reducible or not.
Parameters: - degree (int) – degree
- ctrlpts (list, tuple) – control points
Returns: control points of the degree-reduced shape
Return type: list
-
geomdl.helpers.find_multiplicity(knot, knot_vector, **kwargs)¶ Finds knot multiplicity over the knot vector.
- Keyword Arguments:
tol: tolerance (delta) value for equality checking
Parameters: - knot (float) – knot or parameter,
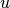
- knot_vector (list, tuple) – knot vector,
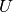
Returns: knot multiplicity,

Return type: int
-
geomdl.helpers.find_span_binsearch(degree, knot_vector, num_ctrlpts, knot, **kwargs)¶ Finds the span of the knot over the input knot vector using binary search.
Implementation of Algorithm A2.1 from The NURBS Book by Piegl & Tiller.
The NURBS Book states that the knot span index always starts from zero, i.e. for a knot vector [0, 0, 1, 1]; if FindSpan returns 1, then the knot is between the half-open interval [0, 1).
Parameters: - degree (int) – degree,
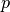
- knot_vector (list, tuple) – knot vector,
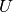
- num_ctrlpts (int) – number of control points,
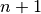
- knot (float) – knot or parameter,
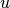
Returns: knot span
Return type: int
- degree (int) – degree,
-
geomdl.helpers.find_span_linear(degree, knot_vector, num_ctrlpts, knot, **kwargs)¶ Finds the span of a single knot over the knot vector using linear search.
Alternative implementation for the Algorithm A2.1 from The NURBS Book by Piegl & Tiller.
Parameters: - degree (int) – degree,
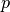
- knot_vector (list, tuple) – knot vector,
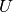
- num_ctrlpts (int) – number of control points,
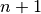
- knot (float) – knot or parameter,
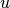
Returns: knot span
Return type: int
- degree (int) – degree,
-
geomdl.helpers.find_spans(degree, knot_vector, num_ctrlpts, knots, func=<function find_span_linear>)¶ Finds spans of a list of knots over the knot vector.
Parameters: - degree (int) – degree,
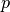
- knot_vector (list, tuple) – knot vector,
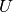
- num_ctrlpts (int) – number of control points,
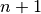
- knots (list, tuple) – list of knots or parameters
- func – function for span finding, e.g. linear or binary search
Returns: list of spans
Return type: list
- degree (int) – degree,
-
geomdl.helpers.knot_insertion(degree, knotvector, ctrlpts, u, **kwargs)¶ Computes the control points of the rational/non-rational spline after knot insertion.
Part of Algorithm A5.1 of The NURBS Book by Piegl & Tiller, 2nd Edition.
- Keyword Arguments:
num: number of knot insertions. Default: 1s: multiplicity of the knot. Default: computed via :func:`.find_multiplicity`span: knot span. Default: computed via :func:`.find_span_linear`
Parameters: - degree (int) – degree
- knotvector (list, tuple) – knot vector
- ctrlpts (list) – control points
- u (float) – knot to be inserted
Returns: updated control points
Return type: list
-
geomdl.helpers.knot_insertion_alpha¶ Computes
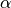 coefficient for knot insertion algorithm.
coefficient for knot insertion algorithm.Parameters: - u (float) – knot
- knotvector (tuple) – knot vector
- span (int) – knot span
- idx (int) – index value (degree-dependent)
- leg (int) – i-th leg of the control points polygon
Returns: coefficient value
Return type: float
-
geomdl.helpers.knot_insertion_kv(knotvector, u, span, r)¶ Computes the knot vector of the rational/non-rational spline after knot insertion.
Part of Algorithm A5.1 of The NURBS Book by Piegl & Tiller, 2nd Edition.
Parameters: - knotvector (list, tuple) – knot vector
- u (float) – knot
- span (int) – knot span
- r (int) – number of knot insertions
Returns: updated knot vector
Return type: list
-
geomdl.helpers.knot_refinement(degree, knotvector, ctrlpts, **kwargs)¶ Computes the knot vector and the control points of the rational/non-rational spline after knot refinement.
Implementation of Algorithm A5.4 of The NURBS Book by Piegl & Tiller, 2nd Edition.
The algorithm automatically find the knots to be refined, i.e. the middle knots in the knot vector, and their multiplicities, i.e. number of same knots in the knot vector. This is the basis of knot refinement algorithm. This operation can be overridden by providing a list of knots via
knot_listargument. In addition, users can provide a list of additional knots to be inserted in the knot vector viaadd_knot_listargument.Moreover, a numerical
densityargument can be used to automate extra knot insertions. Ifdensityis bigger than 1, then the algorithm finds the middle knots in each internal knot span to increase the number of knots to be refined.Example: Let the degree is 2 and the knot vector to be refined is
[0, 2, 4]with the superfluous knots from the start and end are removed. Knot vectors with the changingdensity (d)value will be:d = 1, knot vector[0, 1, 1, 2, 2, 3, 3, 4]d = 2, knot vector[0, 0.5, 0.5, 1, 1, 1.5, 1.5, 2, 2, 2.5, 2.5, 3, 3, 3.5, 3.5, 4]
- Keyword Arguments:
knot_list: knot list to be refined. Default: list of internal knotsadd_knot_list: additional list of knots to be refined. Default: []density: Density of the knots. Default: 1
Parameters: - degree (int) – degree
- knotvector (list, tuple) – knot vector
- ctrlpts – control points
Returns: updated control points and knot vector
Return type: tuple
-
geomdl.helpers.knot_removal(degree, knotvector, ctrlpts, u, **kwargs)¶ Computes the control points of the rational/non-rational spline after knot removal.
Implementation based on Algorithm A5.8 and Equation 5.28 of The NURBS Book by Piegl & Tiller
- Keyword Arguments:
num: number of knot removals
Parameters: - degree (int) – degree
- knotvector (list, tuple) – knot vector
- ctrlpts (list) – control points
- u (float) – knot to be removed
Returns: updated control points
Return type: list
-
geomdl.helpers.knot_removal_alpha_i¶ Computes
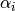 coefficient for knot removal algorithm.
coefficient for knot removal algorithm.Please refer to Eq. 5.29 of The NURBS Book by Piegl & Tiller, 2nd Edition, p.184 for details.
Parameters: - u (float) – knot
- degree (int) – degree
- knotvector (tuple) – knot vector
- num (int) – knot removal index
- idx (int) – iterator index
Returns: coefficient value
Return type: float
-
geomdl.helpers.knot_removal_alpha_j¶ Computes
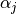 coefficient for knot removal algorithm.
coefficient for knot removal algorithm.Please refer to Eq. 5.29 of The NURBS Book by Piegl & Tiller, 2nd Edition, p.184 for details.
Parameters: - u (float) – knot
- degree (int) – degree
- knotvector (tuple) – knot vector
- num (int) – knot removal index
- idx (int) – iterator index
Returns: coefficient value
Return type: float
-
geomdl.helpers.knot_removal_kv(knotvector, span, r)¶ Computes the knot vector of the rational/non-rational spline after knot removal.
Part of Algorithm A5.8 of The NURBS Book by Piegl & Tiller, 2nd Edition.
Parameters: - knotvector (list, tuple) – knot vector
- span (int) – knot span
- r (int) – number of knot removals
Returns: updated knot vector
Return type: list
-
geomdl.helpers.surface_deriv_cpts(dim, degree, kv, cpts, cpsize, rs, ss, deriv_order=0)¶ Compute control points of surface derivatives.
Implementation of Algorithm A3.7 from The NURBS Book by Piegl & Tiller.
Parameters: - dim (int) – spatial dimension of the surface
- degree (list, tuple) – degrees
- kv (list, tuple) – knot vectors
- cpts (list, tuple) – control points
- cpsize (list, tuple) – number of control points in all parametric directions
- rs (list, tuple) – minimum (r1) and maximum (r2) knot spans for the u-direction
- ss (list, tuple) – minimum (s1) and maximum (s2) knot spans for the v-direction
- deriv_order (int) – derivative order, i.e. the i-th derivative
Returns: control points of the derivative surface over the input knot span ranges
Return type: list
Linear Algebra¶
The linalg module contains some basic functions for point, vector and matrix operations.
Although most of the functions are designed for internal usage, the users can still use some of the functions for their
advantage, especially the point and vector manipulation and generation functions. Functions related to point
manipulation have point_ prefix and the ones related to vectors have vector_ prefix.
-
geomdl.linalg.backward_substitution(matrix_u, matrix_y)¶ Backward substitution method for the solution of linear systems.
Solves the equation
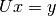 using backward substitution method
where
using backward substitution method
where 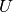 is a upper triangular matrix and
is a upper triangular matrix and 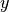 is a column matrix.
is a column matrix.Parameters: - matrix_u (list, tuple) – U, upper triangular matrix
- matrix_y (list, tuple) – y, column matrix
Returns: x, column matrix
Return type: list
-
geomdl.linalg.binomial_coefficient¶ Computes the binomial coefficient (denoted by k choose i).
Please see the following website for details: http://mathworld.wolfram.com/BinomialCoefficient.html
Parameters: - k (int) – size of the set of distinct elements
- i (int) – size of the subsets
Returns: combination of k and i
Return type: float
-
geomdl.linalg.convex_hull(points)¶ Returns points on convex hull in counterclockwise order according to Graham’s scan algorithm.
Reference: https://gist.github.com/arthur-e/5cf52962341310f438e96c1f3c3398b8
Note
This implementation only works in 2-dimensional space.
Parameters: points (list, tuple) – list of 2-dimensional points Returns: convex hull of the input points Return type: list
-
geomdl.linalg.forward_substitution(matrix_l, matrix_b)¶ Forward substitution method for the solution of linear systems.
Solves the equation
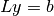 using forward substitution method
where
using forward substitution method
where 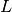 is a lower triangular matrix and
is a lower triangular matrix and 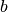 is a column matrix.
is a column matrix.Parameters: - matrix_l (list, tuple) – L, lower triangular matrix
- matrix_b (list, tuple) – b, column matrix
Returns: y, column matrix
Return type: list
-
geomdl.linalg.frange(start, stop, step=1.0)¶ Implementation of Python’s
range()function which works with floats.Reference to this implementation: https://stackoverflow.com/a/36091634
Parameters: - start (float) – start value
- stop (float) – end value
- step (float) – increment
Returns: float
Return type: generator
-
geomdl.linalg.is_left(point0, point1, point2)¶ Tests if a point is Left|On|Right of an infinite line.
Ported from the C++ version: on http://geomalgorithms.com/a03-_inclusion.html
Note
This implementation only works in 2-dimensional space.
Parameters: - point0 – Point P0
- point1 – Point P1
- point2 – Point P2
Returns: >0 for P2 left of the line through P0 and P1 =0 for P2 on the line <0 for P2 right of the line
-
geomdl.linalg.linspace(start, stop, num, decimals=18)¶ Returns a list of evenly spaced numbers over a specified interval.
Inspired from Numpy’s linspace function: https://github.com/numpy/numpy/blob/master/numpy/core/function_base.py
Parameters: - start (float) – starting value
- stop (float) – end value
- num (int) – number of samples to generate
- decimals (int) – number of significands
Returns: a list of equally spaced numbers
Return type: list
-
geomdl.linalg.lu_decomposition(matrix_a)¶ LU-Factorization method using Doolittle’s Method for solution of linear systems.
Decomposes the matrix
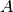 such that
such that 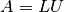 .
.The input matrix is represented by a list or a tuple. The input matrix is 2-dimensional, i.e. list of lists of integers and/or floats.
Parameters: matrix_a (list, tuple) – Input matrix (must be a square matrix) Returns: a tuple containing matrices L and U Return type: tuple
-
geomdl.linalg.lu_factor(matrix_a, b)¶ Computes the solution to a system of linear equations with partial pivoting.
This function solves
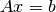 using LUP decomposition.
using LUP decomposition. 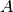 is a
is a
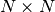 matrix,
matrix, 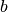 is
is 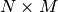 matrix of
matrix of
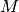 column vectors. Each column of
column vectors. Each column of 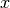 is a solution for
corresponding column of
is a solution for
corresponding column of 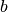 .
.Parameters: - matrix_a – matrix A
- b (list) – matrix of M column vectors
Returns: x, the solution matrix
Return type: list
-
geomdl.linalg.lu_solve(matrix_a, b)¶ Computes the solution to a system of linear equations.
This function solves
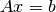 using LU decomposition.
using LU decomposition. 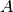 is a
is a
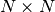 matrix,
matrix, 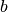 is
is 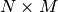 matrix of
matrix of
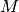 column vectors. Each column of
column vectors. Each column of 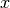 is a solution for
corresponding column of
is a solution for
corresponding column of 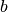 .
.Parameters: - matrix_a – matrix A
- b (list) – matrix of M column vectors
Returns: x, the solution matrix
Return type: list
-
geomdl.linalg.matrix_determinant(m)¶ Computes the determinant of the square matrix
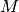 via LUP decomposition.
via LUP decomposition.Parameters: m (list, tuple) – input matrix Returns: determinant of the matrix Return type: float
-
geomdl.linalg.matrix_identity¶ Generates a
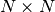 identity matrix.
identity matrix.Parameters: n (int) – size of the matrix Returns: identity matrix Return type: list
-
geomdl.linalg.matrix_inverse(m)¶ Computes the inverse of the matrix via LUP decomposition.
Parameters: m (list, tuple) – input matrix Returns: inverse of the matrix Return type: list
-
geomdl.linalg.matrix_multiply(mat1, mat2)¶ Matrix multiplication (iterative algorithm).
The running time of the iterative matrix multiplication algorithm is
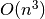 .
.Parameters: - mat1 (list, tuple) – 1st matrix with dimensions
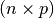
- mat2 (list, tuple) – 2nd matrix with dimensions
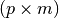
Returns: resultant matrix with dimensions
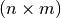
Return type: list
- mat1 (list, tuple) – 1st matrix with dimensions
-
geomdl.linalg.matrix_pivot(m, sign=False)¶ Computes the pivot matrix for M, a square matrix.
This function computes
- the permutation matrix,
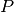
- the product of M and P,
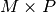
- determinant of P,
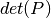 if
if sign = True
Parameters: - m (list, tuple) – input matrix
- sign (bool) – flag to return the determinant of the permutation matrix, P
Returns: a tuple containing the matrix product of M x P, P and det(P)
Return type: tuple
- the permutation matrix,
-
geomdl.linalg.matrix_scalar(m, sc)¶ Matrix multiplication by a scalar value (iterative algorithm).
The running time of the iterative matrix multiplication algorithm is
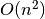 .
.Parameters: - m (list, tuple) – input matrix
- sc (int, float) – scalar value
Returns: resultant matrix
Return type: list
-
geomdl.linalg.matrix_transpose(m)¶ Transposes the input matrix.
The input matrix
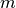 is a 2-dimensional array.
is a 2-dimensional array.Parameters: m (list, tuple) – input matrix with dimensions 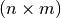
Returns: transpose matrix with dimensions 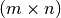
Return type: list
-
geomdl.linalg.point_distance(pt1, pt2)¶ Computes distance between two points.
Parameters: - pt1 (list, tuple) – point 1
- pt2 (list, tuple) – point 2
Returns: distance between input points
Return type: float
-
geomdl.linalg.point_mid(pt1, pt2)¶ Computes the midpoint of the input points.
Parameters: - pt1 (list, tuple) – point 1
- pt2 (list, tuple) – point 2
Returns: midpoint
Return type: list
-
geomdl.linalg.point_translate(point_in, vector_in)¶ Translates the input points using the input vector.
Parameters: - point_in (list, tuple) – input point
- vector_in (list, tuple) – input vector
Returns: translated point
Return type: list
-
geomdl.linalg.triangle_center(tri, uv=False)¶ Computes the center of mass of the input triangle.
Parameters: - tri (elements.Triangle) – triangle object
- uv (bool) – if True, then finds parametric position of the center of mass
Returns: center of mass of the triangle
Return type: tuple
-
geomdl.linalg.triangle_normal(tri)¶ Computes the (approximate) normal vector of the input triangle.
Parameters: tri (elements.Triangle) – triangle object Returns: normal vector of the triangle Return type: tuple
-
geomdl.linalg.vector_angle_between(vector1, vector2, **kwargs)¶ Computes the angle between the two input vectors.
If the keyword argument
degreesis set to True, then the angle will be in degrees. Otherwise, it will be in radians. By default,degreesis set to True.Parameters: - vector1 (list, tuple) – vector
- vector2 (list, tuple) – vector
Returns: angle between the vectors
Return type: float
-
geomdl.linalg.vector_cross(vector1, vector2)¶ Computes the cross-product of the input vectors.
Parameters: - vector1 (list, tuple) – input vector 1
- vector2 (list, tuple) – input vector 2
Returns: result of the cross product
Return type: tuple
-
geomdl.linalg.vector_dot(vector1, vector2)¶ Computes the dot-product of the input vectors.
Parameters: - vector1 (list, tuple) – input vector 1
- vector2 (list, tuple) – input vector 2
Returns: result of the dot product
Return type: float
-
geomdl.linalg.vector_generate(start_pt, end_pt, normalize=False)¶ Generates a vector from 2 input points.
Parameters: - start_pt (list, tuple) – start point of the vector
- end_pt (list, tuple) – end point of the vector
- normalize (bool) – if True, the generated vector is normalized
Returns: a vector from start_pt to end_pt
Return type: list
-
geomdl.linalg.vector_is_zero(vector_in, tol=1e-07)¶ Checks if the input vector is a zero vector.
Parameters: - vector_in (list, tuple) – input vector
- tol (float) – tolerance value
Returns: True if the input vector is zero, False otherwise
Return type: bool
-
geomdl.linalg.vector_magnitude(vector_in)¶ Computes the magnitude of the input vector.
Parameters: vector_in (list, tuple) – input vector Returns: magnitude of the vector Return type: float
-
geomdl.linalg.vector_mean(*args)¶ Computes the mean (average) of a list of vectors.
The function computes the arithmetic mean of a list of vectors, which are also organized as a list of integers or floating point numbers.
1 2 3 4 5 6 7 8
# Create a list of vectors as an example vector_list = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] # Compute mean vector mean_vector = vector_mean(*vector_list) # Alternative usage example (same as above): mean_vector = vector_mean([1, 2, 3], [4, 5, 6], [7, 8, 9])
Parameters: args (list, tuple) – list of vectors Returns: mean vector Return type: list
-
geomdl.linalg.vector_multiply(vector_in, scalar)¶ Multiplies the vector with a scalar value.
This operation is also called vector scaling.
Parameters: - vector_in (list, tuple) – vector
- scalar (int, float) – scalar value
Returns: updated vector
Return type: tuple
-
geomdl.linalg.vector_normalize(vector_in, decimals=18)¶ Generates a unit vector from the input.
Parameters: - vector_in (list, tuple) – vector to be normalized
- decimals (int) – number of significands
Returns: the normalized vector (i.e. the unit vector)
Return type: list
-
geomdl.linalg.vector_sum(vector1, vector2, coeff=1.0)¶ Sums the vectors.
This function computes the result of the vector operation
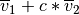 , where
, where
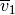 is
is vector1,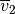 is
is vector2and is
is coeff.Parameters: - vector1 (list, tuple) – vector 1
- vector2 (list, tuple) – vector 2
- coeff (float) – multiplier for vector 2
Returns: updated vector
Return type: list
-
geomdl.linalg.wn_poly(point, vertices)¶ Winding number test for a point in a polygon.
Ported from the C++ version: http://geomalgorithms.com/a03-_inclusion.html
Note
This implementation only works in 2-dimensional space.
Parameters: - point (list, tuple) – point to be tested
- vertices (list, tuple) – vertex points of a polygon vertices[n+1] with vertices[n] = vertices[0]
Returns: True if the point is inside the input polygon, False otherwise
Return type: bool