Ray Module¶

ray module provides utilities for ray operations. A ray (half-line) is defined by two distinct points represented by Ray class. This module also provides a function to compute intersection of 2 rays.

Function and Class Reference¶

class geomdl.ray.Ray(point1, point2)¶

Representation of a n-dimensional ray generated from 2 points.

A ray is defined by 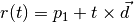$r(t)=p_{1}+t\times\vec{d}$ where :math`t` is the parameter value, 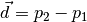$\vec{d} = p_{2}-p_{1}$ is the vector component of the ray, 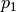$p_{1}$ is the origin point and 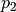$p_{2}$ is the second point which is required to define a line segment

Parameters:	point1 (list, tuple) – 1st point of the line segment point2 (list, tuple) – 2nd point of the line segment

d¶

Vector component of the ray (d)

Please refer to the wiki for details on using this class member.

Getter:	Gets the vector component of the ray

dimension¶

Spatial dimension of the ray

Please refer to the wiki for details on using this class member.

Getter:	Gets the dimension of the ray

eval(t=0)¶

Finds the point on the line segment defined by the input parameter.

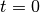$t=0$ returns the origin (1st) point, defined by the input argument point1 and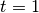 $t=1$ returns the end (2nd) point, defined by the input argument point2.

Parameters:	t (float) – parameter
Returns:	point at the parameter value
Return type:	tuple

p¶

Origin point of the ray (p)

Please refer to the wiki for details on using this class member.

Getter:	Gets the origin point of the ray

points¶

Start and end points of the line segment that the ray was generated

Please refer to the wiki for details on using this class member.

Getter:	Gets the points

class geomdl.ray.RayIntersection¶: The status of the ray intersection operation

geomdl.ray.intersect(ray1, ray2, **kwargs)¶

Finds intersection of 2 rays.

This functions finds the parameter values for the 1st and 2nd input rays and returns a tuple of (parameter for ray1, parameter for ray2, intersection status). status value is a enum type which reports the case which the intersection operation encounters.

The intersection operation can encounter 3 different cases:

Intersecting: This is the anticipated solution. Returns (t1, t2, RayIntersection.INTERSECT)
Colinear: The rays can be parallel or coincident. Returns (t1, t2, RayIntersection.COLINEAR)
Skew: The rays are neither parallel nor intersecting. Returns (t1, t2, RayIntersection.SKEW)

For the colinear case, t1 and t2 are the parameter values that give the starting point of the ray2 and ray1, respectively. Therefore;

ray1.eval(t1) == ray2.p
ray2.eval(t2) == ray1.p

Please note that this operation is only implemented for 2- and 3-dimensional rays.

Parameters:	ray1 – 1st ray ray2 – 2nd ray
Returns:	a tuple of the parameter (t) for ray1 and ray2, and status of the intersection
Return type:	tuple