Geometric Operations¶
This module provides common geometric operations for curves and surfaces. It includes the following operations:
- Knot insertion, removal and refinement
- Curve and surface splitting / Bézier decomposition
- Tangent, normal and binormal evaluations
- Hodograph curve and surface computations
- Translation, rotation and scaling
Function Reference¶
-
geomdl.operations.insert_knot(obj, param, num, **kwargs)¶ Inserts knots n-times to a spline geometry.
The following code snippet illustrates the usage of this function:
# Insert knot u=0.5 to a curve 2 times operations.insert_knot(curve, [0.5], [2]) # Insert knot v=0.25 to a surface 1 time operations.insert_knot(surface, [None, 0.25], [0, 1]) # Insert knots u=0.75, v=0.25 to a surface 2 and 1 times, respectively operations.insert_knot(surface, [0.75, 0.25], [2, 1]) # Insert knot w=0.5 to a volume 1 time operations.insert_knot(volume, [None, None, 0.5], [0, 0, 1])
Please note that input spline geometry object will always be updated if the knot insertion operation is successful.
- Keyword Arguments:
check_num: enables/disables operation validity checks. Default: True
Parameters: - obj (abstract.SplineGeometry) – spline geometry
- param (list, tuple) – knot(s) to be inserted in [u, v, w] format
- num (list, tuple) – number of knot insertions in [num_u, num_v, num_w] format
Returns: updated spline geometry
-
geomdl.operations.remove_knot(obj, param, num, **kwargs)¶ Removes knots n-times from a spline geometry.
The following code snippet illustrates the usage of this function:
# Remove knot u=0.5 from a curve 2 times operations.remove_knot(curve, [0.5], [2]) # Remove knot v=0.25 from a surface 1 time operations.remove_knot(surface, [None, 0.25], [0, 1]) # Remove knots u=0.75, v=0.25 from a surface 2 and 1 times, respectively operations.remove_knot(surface, [0.75, 0.25], [2, 1]) # Remove knot w=0.5 from a volume 1 time operations.remove_knot(volume, [None, None, 0.5], [0, 0, 1])
Please note that input spline geometry object will always be updated if the knot removal operation is successful.
- Keyword Arguments:
check_num: enables/disables operation validity checks. Default: True
Parameters: - obj (abstract.SplineGeometry) – spline geometry
- param (list, tuple) – knot(s) to be removed in [u, v, w] format
- num (list, tuple) – number of knot removals in [num_u, num_v, num_w] format
Returns: updated spline geometry
-
geomdl.operations.refine_knotvector(obj, param, **kwargs)¶ Refines the knot vector(s) of a spline geometry.
The following code snippet illustrates the usage of this function:
# Refines the knot vector of a curve operations.refine_knotvector(curve, [1]) # Refines the knot vector on the v-direction of a surface operations.refine_knotvector(surface, [0, 1]) # Refines the both knot vectors of a surface operations.refine_knotvector(surface, [1, 1]) # Refines the knot vector on the w-direction of a volume operations.refine_knotvector(volume, [0, 0, 1])
The values of
paramargument can be used to set the knot refinement density. If density is bigger than 1, then the algorithm finds the middle knots in each internal knot span to increase the number of knots to be refined.Example: Let the degree is 2 and the knot vector to be refined is
[0, 2, 4]with the superfluous knots from the start and end are removed. Knot vectors with the changingdensity (d)value will be:d = 1, knot vector[0, 1, 1, 2, 2, 3, 3, 4]d = 2, knot vector[0, 0.5, 0.5, 1, 1, 1.5, 1.5, 2, 2, 2.5, 2.5, 3, 3, 3.5, 3.5, 4]
The following code snippet illustrates the usage of knot refinement densities:
# Refines the knot vector of a curve with density = 3 operations.refine_knotvector(curve, [3]) # Refines the knot vectors of a surface with density for # u-dir = 2 and v-dir = 3 operations.refine_knotvector(surface, [2, 3]) # Refines only the knot vector on the v-direction of a surface with density = 1 operations.refine_knotvector(surface, [0, 1]) # Refines the knot vectors of a volume with density for # u-dir = 1, v-dir = 3 and w-dir = 2 operations.refine_knotvector(volume, [1, 3, 2])
Please refer to
helpers.knot_refinement()function for more usage options.- Keyword Arguments:
check_num: enables/disables operation validity checks. Default: True
Parameters: - obj (abstract.SplineGeometry) – spline geometry
- param (list, tuple) – parametric dimensions to be refined in [u, v, w] format
Returns: updated spline geometry
-
geomdl.operations.add_dimension(obj, **kwargs)¶ Elevates the spatial dimension of the spline geometry.
If you pass
inplace=Truekeyword argument, the input will be updated. Otherwise, this function does not change the input but returns a new instance with the updated data.Parameters: obj (abstract.SplineGeometry) – spline geometry Returns: updated spline geometry Return type: abstract.SplineGeometry
-
geomdl.operations.split_curve(obj, param, **kwargs)¶ Splits the curve at the input parametric coordinate.
This method splits the curve into two pieces at the given parametric coordinate, generates two different curve objects and returns them. It does not modify the input curve.
- Keyword Arguments:
find_span_func: FindSpan implementation. Default:helpers.find_span_linear()insert_knot_func: knot insertion algorithm implementation. Default:operations.insert_knot()
Parameters: - obj (abstract.Curve) – Curve to be split
- param (float) – parameter
Returns: a list of curve segments
Return type: list
-
geomdl.operations.decompose_curve(obj, **kwargs)¶ Decomposes the curve into Bezier curve segments of the same degree.
This operation does not modify the input curve, instead it returns the split curve segments.
- Keyword Arguments:
find_span_func: FindSpan implementation. Default:helpers.find_span_linear()insert_knot_func: knot insertion algorithm implementation. Default:operations.insert_knot()
Parameters: obj (abstract.Curve) – Curve to be decomposed Returns: a list of Bezier segments Return type: list
-
geomdl.operations.derivative_curve(obj)¶ Computes the hodograph (first derivative) curve of the input curve.
This function constructs the hodograph (first derivative) curve from the input curve by computing the degrees, knot vectors and the control points of the derivative curve.
Parameters: obj (abstract.Curve) – input curve Returns: derivative curve
-
geomdl.operations.length_curve(obj)¶ Computes the approximate length of the parametric curve.
Uses the following equation to compute the approximate length:
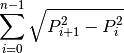
where
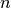 is number of evaluated curve points and
is number of evaluated curve points and 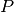 is the n-dimensional point.
is the n-dimensional point.Parameters: obj (abstract.Curve) – input curve Returns: length Return type: float
-
geomdl.operations.split_surface_u(obj, param, **kwargs)¶ Splits the surface at the input parametric coordinate on the u-direction.
This method splits the surface into two pieces at the given parametric coordinate on the u-direction, generates two different surface objects and returns them. It does not modify the input surface.
- Keyword Arguments:
find_span_func: FindSpan implementation. Default:helpers.find_span_linear()insert_knot_func: knot insertion algorithm implementation. Default:operations.insert_knot()
Parameters: - obj (abstract.Surface) – surface
- param (float) – parameter for the u-direction
Returns: a list of surface patches
Return type: list
-
geomdl.operations.split_surface_v(obj, param, **kwargs)¶ Splits the surface at the input parametric coordinate on the v-direction.
This method splits the surface into two pieces at the given parametric coordinate on the v-direction, generates two different surface objects and returns them. It does not modify the input surface.
- Keyword Arguments:
find_span_func: FindSpan implementation. Default:helpers.find_span_linear()insert_knot_func: knot insertion algorithm implementation. Default:operations.insert_knot()
Parameters: - obj (abstract.Surface) – surface
- param (float) – parameter for the v-direction
Returns: a list of surface patches
Return type: list
-
geomdl.operations.decompose_surface(obj, **kwargs)¶ Decomposes the surface into Bezier surface patches of the same degree.
This operation does not modify the input surface, instead it returns the surface patches.
- Keyword Arguments:
find_span_func: FindSpan implementation. Default:helpers.find_span_linear()insert_knot_func: knot insertion algorithm implementation. Default:operations.insert_knot()
Parameters: obj (abstract.Surface) – surface Returns: a list of Bezier patches Return type: list
-
geomdl.operations.derivative_surface(obj)¶ Computes the hodograph (first derivative) surface of the input surface.
This function constructs the hodograph (first derivative) surface from the input surface by computing the degrees, knot vectors and the control points of the derivative surface.
The return value of this function is a tuple containing the following derivative surfaces in the given order:
- U-derivative surface (derivative taken only on the u-direction)
- V-derivative surface (derivative taken only on the v-direction)
- UV-derivative surface (derivative taken on both the u- and the v-direction)
Parameters: obj (abstract.Surface) – input surface Returns: derivative surfaces w.r.t. u, v and both u-v Return type: tuple
-
geomdl.operations.find_ctrlpts(obj, u, v=None, **kwargs)¶ Finds the control points involved in the evaluation of the curve/surface point defined by the input parameter(s).
Parameters: - obj (abstract.Curve or abstract.Surface) – curve or surface
- u (float) – parameter (for curve), parameter on the u-direction (for surface)
- v (float) – parameter on the v-direction (for surface only)
Returns: control points; 1-dimensional array for curve, 2-dimensional array for surface
Return type: list
-
geomdl.operations.tangent(obj, params, **kwargs)¶ Evaluates the tangent vector of the curves or surfaces at the input parameter values.
This function is designed to evaluate tangent vectors of the B-Spline and NURBS shapes at single or multiple parameter positions.
Parameters: - obj (abstract.Curve or abstract.Surface) – input shape
- params (float, list or tuple) – parameters
Returns: a list containing “point” and “vector” pairs
Return type: tuple
-
geomdl.operations.normal(obj, params, **kwargs)¶ Evaluates the normal vector of the curves or surfaces at the input parameter values.
This function is designed to evaluate normal vectors of the B-Spline and NURBS shapes at single or multiple parameter positions.
Parameters: - obj (abstract.Curve or abstract.Surface) – input geometry
- params (float, list or tuple) – parameters
Returns: a list containing “point” and “vector” pairs
Return type: tuple
-
geomdl.operations.translate(obj, vec, **kwargs)¶ Translates curves, surface or volumes by the input vector.
- Keyword Arguments:
inplace: if False, operation applied to a copy of the object. Default: False
Parameters: - obj (abstract.SplineGeometry or multi.AbstractContainer) – input geometry
- vec (list, tuple) – translation vector
Returns: translated geometry object
-
geomdl.operations.rotate(obj, angle, **kwargs)¶ Rotates curves, surfaces or volumes about the chosen axis.
- Keyword Arguments:
axis: rotation axis; x, y, z correspond to 0, 1, 2 respectively. Default: 2inplace: if False, operation applied to a copy of the object. Default: False
Parameters: - obj (abstract.SplineGeometry, multi.AbstractGeometry) – input geometry
- angle (float) – angle of rotation (in degrees)
Returns: rotated geometry object
-
geomdl.operations.scale(obj, multiplier, **kwargs)¶ Scales curves, surfaces or volumes by the input multiplier.
- Keyword Arguments:
inplace: if False, operation applied to a copy of the object. Default: False
Parameters: - obj (abstract.SplineGeometry, multi.AbstractGeometry) – input geometry
- multiplier (float) – scaling multiplier
Returns: scaled geometry object
-
geomdl.operations.transpose(surf, **kwargs)¶ Transposes the input surface(s) by swapping u and v parametric directions.
- Keyword Arguments:
inplace: if False, operation applied to a copy of the object. Default: False
Parameters: surf (abstract.Surface, multi.SurfaceContainer) – input surface(s) Returns: transposed surface(s)
-
geomdl.operations.flip(surf, **kwargs)¶ Flips the control points grid of the input surface(s).
- Keyword Arguments:
inplace: if False, operation applied to a copy of the object. Default: False
Parameters: surf (abstract.Surface, multi.SurfaceContainer) – input surface(s) Returns: flipped surface(s)